Critical time-dependent branching process modelling epidemic spreading with containment measures
Abstract
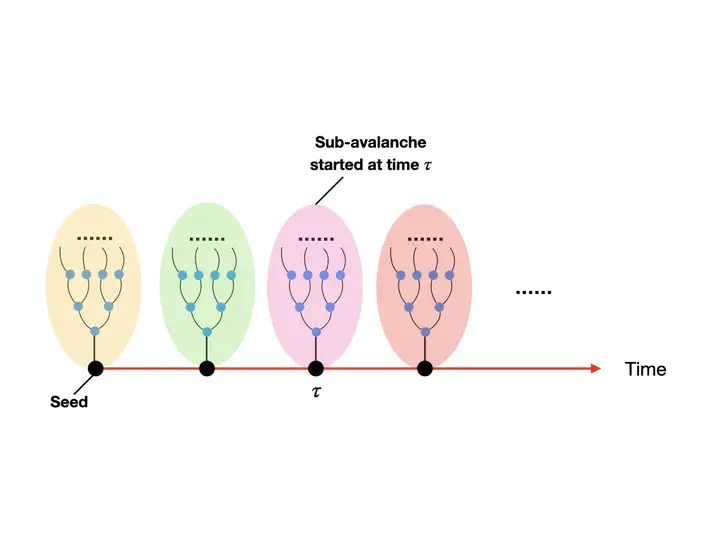
During the COVID pandemic, periods of exponential growth of the disease have been mitigated by containment measures that in different occasions have resulted in a power-law growth of the number of cases. The first observation of such behaviour has been obtained from 2020 late spring data coming from China by Ziff and Ziff in reference Ziff and Ziff (2020 Fractal kinetics of COVID-19 pandemic MedRxiv). After this important observation the power-law scaling (albeit with different exponents) has also been observed in other countries during periods of containment of the spread. Early interpretations of these results suggest that this phenomenon might be due to spatial effects of the spread. Here we show that temporal modulations of infectivity of individuals due to containment measures can also cause power-law growth of the number of cases over time. To this end we propose a stochastic well-mixed susceptible-infected-removed model of epidemic spreading in presence of containment measures resulting in a time dependent infectivity and we explore the statistical properties of the resulting branching process at criticality. We show that at criticality it is possible to observe power-law growth of the number of cases with exponents ranging between one and two. Our asymptotic analytical results are confirmed by extensive Monte Carlo simulations. Although these results do not exclude that spatial effects might be important in modulating the power-law growth of the number of cases at criticality, this work shows that even well-mixed populations may already feature non trivial power-law exponents at criticality.