Abstract
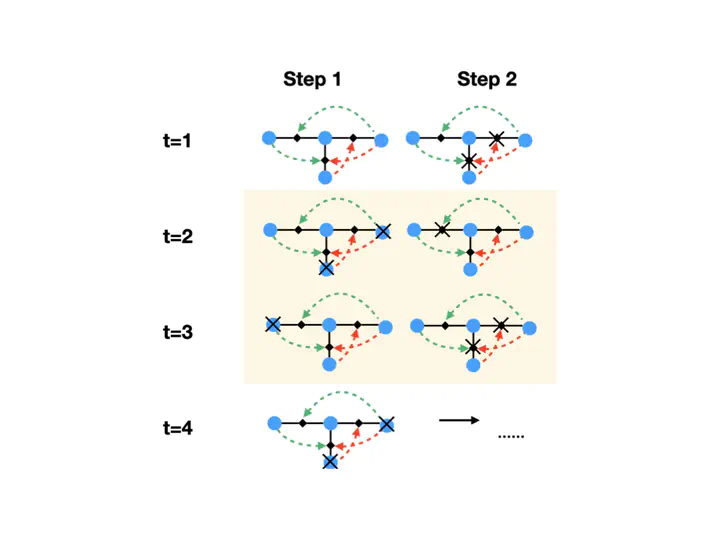
Percolation establishes the connectivity of complex networks and is one of the most fundamental critical phenomena for the study of complex systems. On simple networks, percolation displays a second-order phase transition; on multiplex networks, the percolation transition can become discontinuous. However, little is known about percolation in networks with higher-order interactions. Here, we show that percolation can be turned into a fully fledged dynamical process when higher-order interactions are taken into account. By introducing signed triadic interactions, in which a node can regulate the interactions between two other nodes, we define triadic percolation. We uncover that in this paradigmatic model the connectivity of the network changes in time and that the order parameter undergoes a period doubling and a route to chaos. We provide a general theory for triadic percolation which accurately predicts the full phase diagram on random graphs as confirmed by extensive numerical simulations. We find that triadic percolation on real network topologies reveals a similar phenomenology. These results radically change our understanding of percolation and may be used to study complex systems in which the functional connectivity is changing in time dynamically and in a non-trivial way, such as in neural and climate networks.