Hanlin Sun

Wallenberg Initiative on Networks and Quantum Information (WINQ) Research Fellow

NORDITA, Stockholm University and KTH Royal Institute of Technologty

Biography

Hanlin is a research fellow at NORDITA, Stockholm University and KTH Royal Institute of Technology, Sweden funded by Wallenberg Initiative on Networks and Quantum Information (WINQ). He is interested in the dynamic processes on networks and higher-order network, inference and optimization on networks, as well as the interdisplinary area between network science and neuroscience.

Hanlin holds a Ph.D. in Applied Mathematics. During his PhD at Queen Mary University of London, he worked on network theory. His research focuses on several aspects of dynamic processes on networks and other structures with higher-order interactions, such as simplicial complexes and hypergraphs, under the supervision of Prof. Ginestra Bianconi.

Before joining Queen Mary, Hanlin studied physics at the University of Chinese Academy of Sciences, China (BSc). During his undergraduate study, he worked on the inference and optimization on multiple interacting spreading processes on networks under the supervisor of Prof. David Saad, Aston University, and low-rank approximation algorithms on tensor networks under the supervisor of Prof. Pan Zhang, Institute of Theoretical Physics, Chinese Academy of Sciences.

Download my CV.

Interests

Percolation theory
Message-passing algorithm
Hypergraphs and simplicial complexes
Epidemic spreading
Statistical Physics
Inference and Optimization on networks
Multilayer networks
Quantum networks

Education

PhD in Applied Mathematics, 2023
Queen Mary University of London, UK
BSc in Physics, 2019
University of Chinese Academy of Sciences, China
Visiting student, 2018
KTH Royal Institute of Technology, Sweden
Visiting student, 2018
Aston University, UK

News

18/09/2024 I start my research visit at Indiana University Bloomington supervised by Prof. Filippo Radicchi, funded by AccelNet-MultiNet Exchange Program.

Experience

AccelNet-MultiNet Fellow

Indiana University

Sep 2024 – Dec 2024 Bloomington, Indiana, US

Research fellow funded by AccelNet-MultiNet program.

WINQ Research fellow

NORDITA, Stockholm University and KTH Royal Institute of Technology

Sep 2023 – Present Stockholm, Sweden

Research fellow funded by The Wallenberg Initiative on Networks and Quantum Information (WINQ).

PhD researcher

Queen Mary University of London

Sep 2019 – Aug 2023 London, United Kingdom

PhD in Applied Mathematics. Study percolation on networks and higher-order structures under the supervision of Prof. Ginestra Bianconi.

Visiting student

Aston University

Jul 2018 – Aug 2018 Birmingham, United Kingdom

Study the inference and optimization on multiple interacting spreading processes under the supervision of Prof. David Saad.

Visiting student

KTH Royal Institute of Technology

Jan 2018 – Jun 2018 Stockholm, Sweden

Course project on Parallel Computing, Artificial Neural Networks and Deep Learning.

Visiting student

Institute of Theoretical Physics, Chinese Academy of Sciences

Jun 2017 – Jan 2018 Beijing, China

Study low-rank approximation algorithms on tensor networks under the supervision of Prof. Pan Zhang.

BSc in Physics

University of Chinese Academy of Sciences

Sep 2015 – Jul 2019 Beijing, China

Activities

Teaching

I will teach Statistical Methods in Data Analysis at the University of Iceland as a Guest Lecturer in Spring 2025.

I have been a Teaching Associate at Queen Mary University of London for the following course:

Vectors and Matrices, Level 4 module, Jan 2023-Apr 2023
Calculus II, Level 4 module, Jan 2023-Apr 2023
Calculus I, Level 4 module, Sep 2022-Dec 2022
Calculus I, Level 4 module, Sep 2021-Dec 2021
Machine Learning with Python, Level 7 module, Jun 2021-Aug 2021
Calculus II, Level 4 module, Jan 2021-Apr 2021
Calculus I, Level 4 module, Sep 2020-Dec 2020
Linear Algebra I, Level 5 module, Sep 2022-Dec 2022
Vectors and Matrices, Level 4 module, Jan 2020-Apr 2020

I have been a Graduate Teaching Assistant at King’s College London for the following course:

Calculus II, Level 4 module, Jan 2023-Apr 2023
Theory of Complex Networks, Level 7 module, Sep 2022-Dec 2022
Linear Algebra and Geometry II, Level 5 module, Jan 2022-Apr 2022
Calculus I, Level 4 module, Sep 2021-Dec 2021

Conferences, Schools and Events

I have been an organiser of the following events:

WINQ program on Complex and Quantum Systems
- A one-week workshop at NORDITA focusing on the Dynamics and Topology of Complex Network Systems.
NetPLACE @ NetSciX 2024
- Panel discussions at NetSciX 2024 on scientific communication.
NetPLACE @ NetSci 2023
- Two panel discussions at NetSci 2023 on some common concerns about academic writing and mental health.
DERI PhD forum
- A seminar at the Digital Environment Research Institute, Queen Mary University of London
NetPlace
- A seminar of Network, Phd Life And ComplExity

I have given contributed and invited talks on the following conferences:

2025 International Workshop “Higher-order interactions: mechanisms, behaviors, and networks” (Erice, Italy)
- Invited plenary lecturer.
2024 Workshop “Quantitative Methods for Dynamics on Networks”, Los Alamos National Laboratory (Los Alamos, US]
- Invited talk. Title: The dynamic nature of percolation on networks with triadic interactions
2024 Isaac Newton Institute Satellite Programme on “Hypergraphs: theory and applications” (London, UK)
- Invited talk. Title: The dynamic nature of percolation on networks with triadic interactions
2024 1st British NetSci Symposium (London, UK)
- Contributed talk. Title: Triadic percolation induces dynamical topological patterns in higher-order networks
2024 APS March Meeting 2024 (Minneapolis, United States)
- Contributed talk. Title: Network science Ising state of matter
2023 CCS/Italy 2023 (Naples, Italy)
- Contributed talk. Title: The dynamic nature of percolation on networks with triadic interactions
2023 NetSci 2023 (Vienna, Austria)
- Contributed talk. Title: The dynamic nature of percolation on networks with triadic interactions
2022 Conference on Complex Systems 2022 (Palma de Mallorca, Spain)
- Contributed talk. Title: Triadic interactions induce blinking and chaos in connectivity of higher-order networks
2022 4th IMA Conference on The Mathematical Challenges of Big Data (Oxford, United Kingdom)
- Contributed talk. Title: A message-passing approach to epidemic tracing and mitigation with apps
2022 Satellite @ NetSci2022: Signed Networks and their Applications (Online)
- Invited talk. Title: Triadic interactions induce blinking and chaos in connectivity of higher-order networks
2022 Satellite @ NetSci2022: Higher-order Topology & Dynamics in Complex Networks (Online)
- Contributed talk. Title: Higher-order percolation processes on multiplex hypergraphs
2021 Conference on Complex Systems 2021 (Lyon, France)
- Contributed talk. Title: Higher-order percolation processes on multiplex hypergraphs
2021 Satellite @ NetSci 2021: TopoNet2021 (Online)
- Contributed talk. Title: Higher-order percolation processes on multiplex hypergraphs
2021 46th Conference of the Middle European Cooperation in Statistical Physics (Online)
- Contributed talk. Title: A message-passing approach to epidemic tracing and mitigation with apps
2020 Conference on Complex Systems 2020 (Online)
- Contributed talk. Title: A message-passing approach to epidemic tracing and mitigation with apps –>

I have also given talks on other internal seminars:

2024 Carlos I Institute of Theoretical and Computational Physics, University of Granada
- Invited talk. Title: Triadic percolation induces dynamical topological patterns in higher-order networks
2023 Applied CATS Seminar, KTH (Stockholm, Sweden)
- Invited talk. Title: Network science Ising states of matter
2023 Internal Seminar, Institute of Theoretical Physics, Chinese Academy of Sciences
- Invited talk. Title: The dynamic nature of percolation on networks with triadic interactions
2023 Internal Seminar, Aston University
- Invited talk. Title: The dynamic nature of percolation on networks with triadic interactions
2023 NetPLACE Seminar
- Invited talk. Title: Message-passing approach to epidemic tracing and mitigation with apps
2023 Networks and Time Workshop, Queen Mary University of London
- Contributed talk. Title: Triadic interactions induce blinking and chaos in connectivity of higher-order networks
2022 Complex Systems Seminar, Queen Mary University of London
- Invited talk. Title: Mathematics in epidemic spreading: from containment measures to critical behaviours
2022 Postgraduate Research Day 2022, Queen Mary University of London
- Talk. Title: Triadic interactions induce blinking and chaos in connectivity of higher-order networks
2022 Internal Seminar, Aston University
- Invited talk. Title: Mathematics in epidemic spreading: from containment measures to critical behaviours
2021 Postgraduate Research Day 2021, Queen Mary University of London
- Poster presentation. Title: A message-passing approach to epidemic tracing and mitigation with apps
2020 Queen Mary Internal Postgraduate Seminar (QuIPS)
- Invited talk. Title: A message-passing approach to epidemic tracing and mitigation with apps

Scholarships and Grants

2024 Visiting Research Scholar, AccelNet/MultiNet Exchange program, $8000
2023 INI Network Support funding, Isaac Newton Institute for Mathematical Sciences, £5000 (with Silvia Rognone, Gabriele Di Bona, Annalisa Caligiuri)
2022 Small Grant, The Institute of Mathematics and its application, £600
2022 Student Grants, Conference on Complex Systems 2022, Fee waiver (equivalently €340)
2022 Research Support Funding, QMUL, £1000
2021 Travel Grant Complex Systems & Networks Group, QMUL, £700
2020 Travel Grant Complex Systems & Networks Group, QMUL, £300

Awards and Achievements

2023 The article ‘The dynamic nature of percolation on networks with triadic interaction’ is featured in Nature Communications Editors’ Highlight
2022 Outstanding Teaching Assistant (Nomination), King’s College London
2021 Press coverage, Competition and collaboration: Understanding interacting epidemics can unlock better disease forecasts, Los Alamos National Laboratory
2021 Press coverage,Competition and Collaboration: Understanding Interacting Epidemics Can Unlock Better Disease Forecasts, Discover Magazine

Referee and editorial activities

I have been a reviewer for the following journals: Physical Review E, Nature Communication, Nature Physics, Physica A: Statistical Mechanics and its Applications, Communication Physics, Scientific Reports, New Journal of Physics, IEEE Transactions on Network Science and Engineering, Bioinformatics, Chaos Solitons and Fractals, Journal of Physics A: Mathematical and Theoretical, Chaos: An Interdisciplinary journal of Nonlinear Science

I served as a Guest Editor Assistant of the Special Issue “Models, Topology and Inference of Multilayer and Higher-Order Networks” in Entropy.

Featured Publications

Hanlin Sun, Filippo Radicchi, Juergen Kurths, Ginestra Bianconi

March, 2023 In Nat Commun

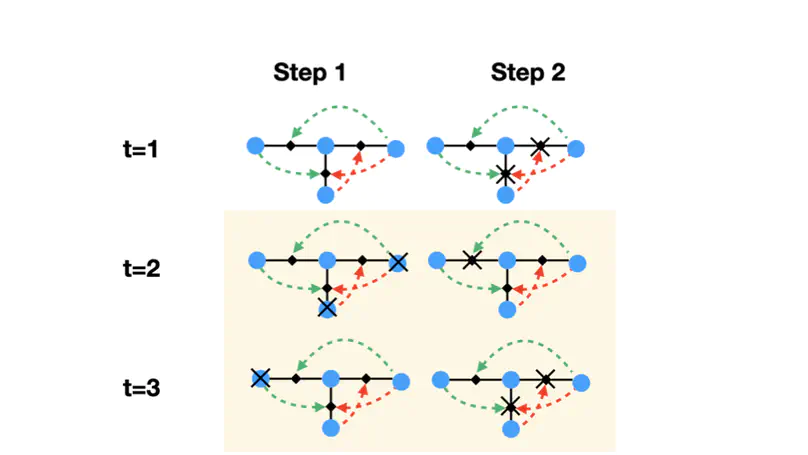
The dynamic nature of percolation on networks with triadic interactions

Percolation establishes the connectivity of complex networks and is one of the most fundamental critical phenomena for the study of complex systems. On simple networks, percolation displays a second-order phase transition; on multiplex networks, the percolation transition can become discontinuous. However, little is known about percolation in networks with higher-order interactions. Here, we show that percolation can be turned into a fully fledged dynamical process when higher-order interactions are taken into account. By introducing signed triadic interactions, in which a node can regulate the interactions between two other nodes, we define triadic percolation. We uncover that in this paradigmatic model the connectivity of the network changes in time and that the order parameter undergoes a period doubling and a route to chaos. We provide a general theory for triadic percolation which accurately predicts the full phase diagram on random graphs as confirmed by extensive numerical simulations. We find that triadic percolation on real network topologies reveals a similar phenomenology. These results radically change our understanding of percolation and may be used to study complex systems in which the functional connectivity is changing in time dynamically and in a non-trivial way, such as in neural and climate networks.

Ginestra Bianconi, Hanlin Sun, Giacomo Rapisardi, Alex Arenas

February, 2021 In Phys. Rev. Res

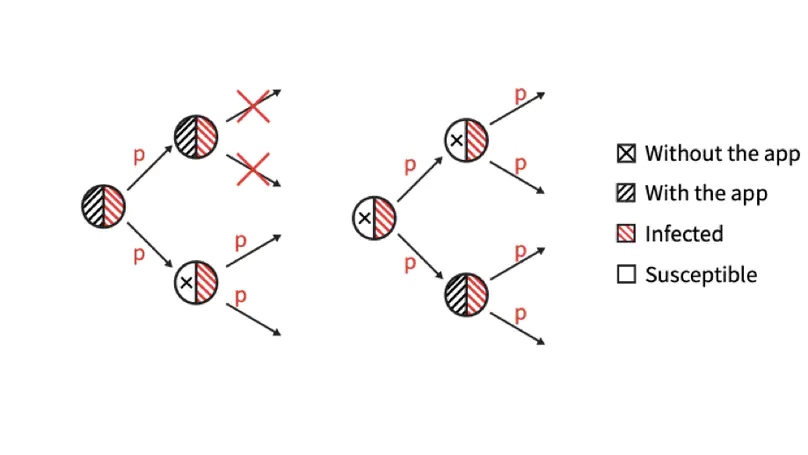
Message-passing approach to epidemic tracing and mitigation with apps

With the hit of new pandemic threats, scientific frameworks are needed to understand the unfolding of the epidemic. The use of mobile apps that are able to trace contacts is of utmost importance in order to control new infected cases and contain further propagation. Here we present a theoretical approach using both percolation and message-passing techniques, to the role of contact tracing, in mitigating an epidemic wave. We show how the increase of the app adoption level raises the value of the epidemic threshold, which is eventually maximized when high-degree nodes are preferentially targeted. Analytical results are compared with extensive Monte Carlo simulations showing good agreement for both homogeneous and heterogeneous networks. These results are important to quantify the level of adoption needed for contact-tracing apps to be effective in mitigating an epidemic.

Hanlin Sun, David Saad, Andrey Y. Lokhov

January, 2021 In Phys. Rev. X

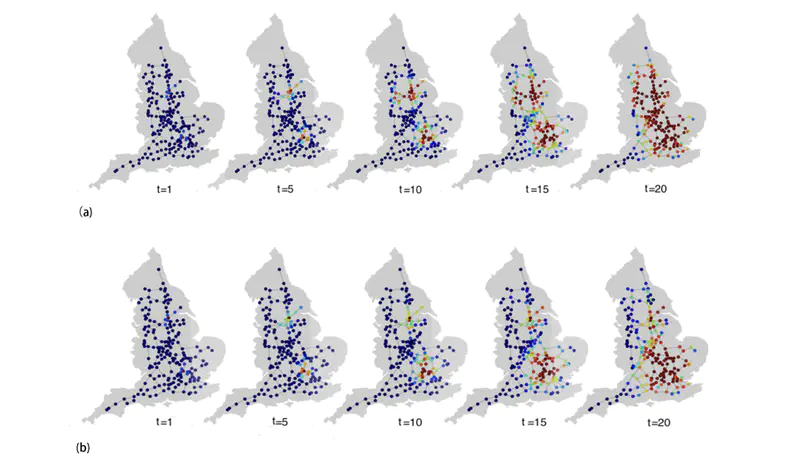
Competition, Collaboration, and Optimization in Multiple Interacting Spreading Processes

Competition and collaboration are at the heart of multiagent probabilistic spreading processes. The battle for public opinion and competitive marketing campaigns are typical examples of the former, while the joint spread of multiple diseases such as HIV and tuberculosis demonstrates the latter. These spreads are influenced by the underlying network topology, the infection rates between network constituents, recovery rates, and, equally important, the interactions between the spreading processes themselves. Here, for the first time, we derive dynamic message-passing equations that provide an exact description of the dynamics of two, interacting, unidirectional spreading processes on tree graphs, and we develop systematic low-complexity models that predict the spread on general graphs. We also develop a theoretical framework for the optimal control of interacting spreading processes through optimized resource allocation under budget constraints and within a finite time window. Derived algorithms can be used to maximize the desired spread in the presence of a rival competitive process and to limit the spread through vaccination in the case of coupled infectious diseases. We demonstrate the efficacy of the framework and optimization method on both synthetic and real-world networks.